说说数学中神奇的斐波那契数列由长春新东方同步长春新东方整理发布，更多精彩内容，请持续关注长春新东方官方网站及长春新东方学校公众号【ccxdfcn】。

　　找规律填数字，这个小学阶段常见的问题，相信陪宝贝写过数学作业的爸爸妈妈们都很熟悉吧?这类问题重在培养小朋友观察、推理、发现规律的能力。

　　关于这个问题很多爸爸妈妈有自己丰富的经验：在小朋友学会按正常的顺序数数之后，可以在生活中变换不同的方式来数数，比如：

　　① 爬楼梯，上楼时可以每上一步加两个数，即1、3、5、7、……，这样奇数数列就有了;② 也可以每上一步加3个数，即1、4、7、10、13……③ 甚至每上一步加4个数，即1、5、9、13……，慢慢地等差数列的概念就初步形成了;④ 至于倒着数，下楼的时候可以从100开始，每下一步减2个数，100、98、96、94、92……一个倒序的偶数数列也产生了。

　　看起来一切都那么美好，那么我们来做做这个数列吧：1、1、2、3、5、8、( )、( )

　　额……好像这道题有些困难啊，它怎么不是常见的等差数列或者奇偶数数列呢?是的，这个奇特的数列叫斐波那契数列(Fibonacci sequence)，又称黄金分割数列。

　　神奇的斐波那契数列

　　斐波那契数列指的是这样一个数列：1，1，2，3，5，8，13，21，34，55，89，144，233，377，610，987，1597，2584，4181，6765，10946，17711，28657，46368...

　　这个数列从第3项开始，每一项都等于前两项之和。

　　斐波那契数列(Fibonacci sequence)，又称黄金分割数列,因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入，故又称为“兔子数列”。

　　为什么是“兔子数列”呢?

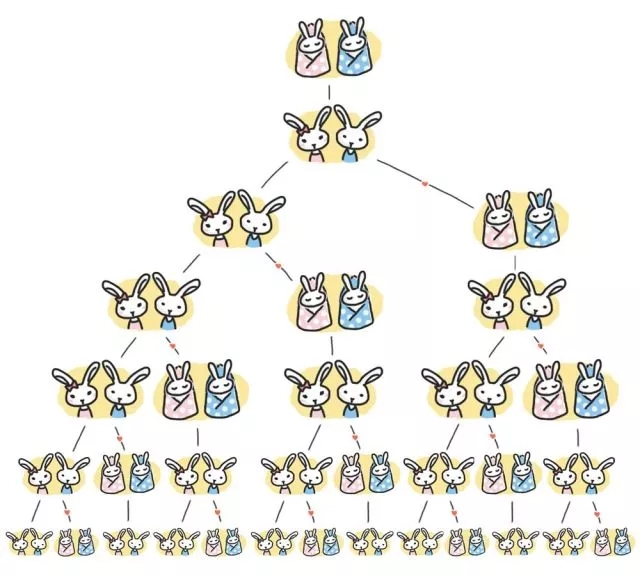
　　我们假设兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。第一个月我们有一对小兔子，如果所有兔子都不死，那么每个月的兔子对数，就符合斐波那契数列。

　　为什么是“黄金分割数列”呢?

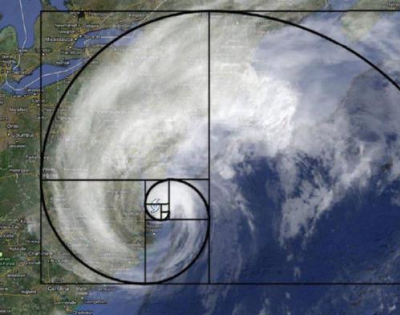
　　随着数列项数的增加，前一项与后一项之比会越来越逼近黄金分割的数值0.6180339887..…

　　黄金比例很重要，它嵌入了无数古代文明的建筑中，包括帕特农神庙和大金字塔。但这并不仅限于数学和建筑，黄金比例影响着我们的日常生活，甚至影响着我们的心理。几项研究发现，人类最容易被五官是黄金比例的面孔所吸引。

　　那么我们如何在自然界寻找斐波那契数列呢?来一起探索大自然的奥秘吧!

　　1葵花

　　例如，在树木的枝干上选一片叶子，记其为数0，然后依序点数叶子(假定没有折损)，直到到达与那些叶子正对的位置，则其间的叶子数多半是斐波那契数。叶子从一个位置到达下一个正对的位置称为一个循回。叶子在一个循回中旋转的圈数也是斐波那契数。在一个循回中叶子数与叶子旋转圈数的比称为叶序(源自希腊词，意即叶子的排列)比。多数的叶序比呈现为斐波那契数的比。

　　2树木

　　例如，在树木的枝干上选一片叶子，记其为数0，然后依序点数叶子(假定没有折损)，直到到达与那些叶子正对的位置，则其间的叶子数多半是斐波那契数。叶子从一个位置到达下一个正对的位置称为一个循回。叶子在一个循回中旋转的圈数也是斐波那契数。在一个循回中叶子数与叶子旋转圈数的比称为叶序(源自希腊词，意即叶子的排列)比。多数的叶序比呈现为斐波那契数的比。

　　3百合花

　　以上就是本文的全部内容，更多精彩内容，请持续关注长春新东方网。