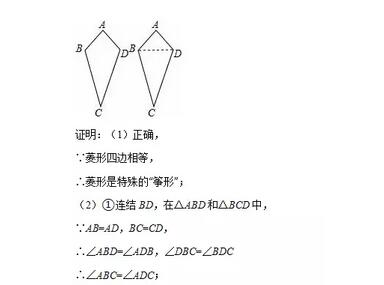
研究几何图形，我们往往先给出这类图形的定义，再研究它的性质和判定方法.我们给出如下定义：如图，四边形ABCD中，AB=AD，CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;

　　(1)小文认为菱形是特殊的“筝形”，你认为他的判断正确吗?

　　(2)小文根据学习几何图形的经验，通过观察、实验、归纳、类比、猜想、证明等方法，对AB≠BC的“筝形”的性质和判定方法进行了探究.下面是小文探究的过程，请补充完成：

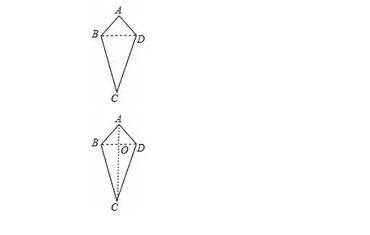
　　①他首先发现了这类“筝形”有一组对角相等，并进行了证明，请你完成小文的证明过程.

　　已知：如图，在”筝形”ABCD中，AB=AD，CB=CD.

　　求证：∠ABC=∠ADC.

　　证明：

　　②小文由①得到了这类“筝形”角的性质，他进一步探究发现这类“筝形”还具有其它性质，请再写出这类“筝形”的一条性质(除“筝形”的定义外)　 　;

　　③继性质探究后，小文探究了这类“筝形”的判定方法，写出这类“筝形”的一条判定方法(除“筝形”的定义外)：

　　②“筝形”有一条对角线平分一组对角(答案不唯一)，

　　连接AC，BD，

　　∵AB=AD，

　　∴A在BD的垂直平分线上，

　　∵BC=DC，

　　∴C在BD的垂直平分线上，

　　∴AC是BD的垂直平分线，

　　∵AB=AD，BC=CD，

　　∴AC平分∠BAC和∠BCD，

　　∴“筝形”有一条对角线平分一组对角，

　　故答案为：“筝形”有一条对角线平分一组对角;

　　③有一条对角线垂直平分另一条对角线的四边形是筝形(答案不唯一).

　　故答案为：有一条对角线垂直平分另一条对角线的四边形是筝形.

　　考点分析：

　　四边形综合题.

　　题干分析：

　　(1)菱形四边相等，根据筝形定义可得菱形是特殊的“筝形”;

　　(2)①连结BD，根据等边对等角可得∠ABD=∠ADB，∠DBC=∠BDC，进而可得∠ABC=∠ADC;

　　②连接AC，BD，根据线段垂直平分线的判定可得AC是BD的垂直平分线，根据等腰三角形三线合一的性质可得AC平分∠BAC和∠BCD;

　　③根据线段垂直平分线的性质可得如果AC是BD的垂直平分线，则AB=AD，BC=CD.

　　解题反思：

　　此题主要考查了四边形的综合，关键是掌握等腰三角形的性质，以及等腰三角形的判定：等边对等角.到线段两端点距离相等的点在线段的垂直平分线上.

       以上就是本文的全部内容，更多精彩请随时关注新东方长春学校官网。

相关推荐

优能中学一对一

优能中学课程

长春初高中学习交流群

　　以上就是本文的全部内容，更多精彩内容，请持续关注长春新东方网。