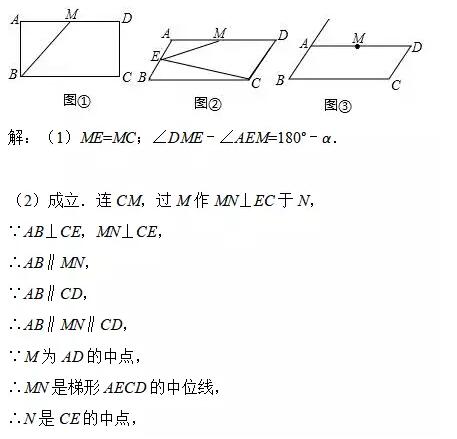
在□ABCD中，BC=2AB，M为AD的中点，设∠ABC=α，过点C作直线AB的垂线，垂足为点E，连ME.

　　(1)如图①，当α=90°，ME与MC的数量关系是____________;

　　∠AEM与∠DME的关系是____________;

　　(2)如图②，当60°<α<90°时，请问：

　　(1)中的两个结论是否仍然成立?若成立，请证明;若不成立，请说明理由;

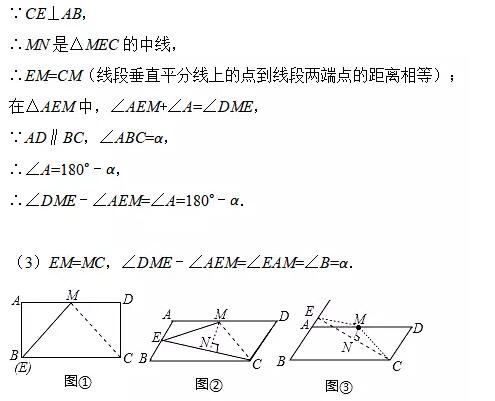
　　(3)如图③，当0°<α<60°时，请在图中画出图形，ME与MC的数量关系是___________;

　　∠AEM与∠DME的关系是___________.(直接写出结论即可，不必证明)

　　考点分析：

　　平行四边形的性质;平行线的性质;三角形的外角性质;线段垂直平分线的性质;综合题;探究型.

　　题干分析：

　　(1)根据α=90°，□ABCD是矩形，又M为AD的中点，所以可以证明△ABM与△DCM是全等三角形，根据全等三角形对应边相等即可得到ME=MC;根据三角形外角性质，∠DME﹣∠AEB=∠A，再根据两直线平行，同旁内角互补，∠A=180°﹣α;

　　(2)点E在线段AB上，过M作MN⊥EC于N，根据M为AD的中点，可得出MN是梯形AECD的中位线，故点N是EC的中点，从而MN是线段EC的垂直平分线，所以ME=MC;先根据两直线平行，同旁内角互补求出∠A的度数，再根据三角形的外角性质即可得到两角的关系.

　　(3)点E在线段BA的延长线上，根据(2)的证明求解方法，同理可解.

　　解题反思：

　　本题主要考查平行四边形的性质和三角形的一个外角等于和它不相邻的两个内角的和的性质以及两直线平行，同旁内角互补的性质，熟练掌握性质并灵活运用是解题的关键。

       以上就是本文的全部内容，更多精彩请随时关注新东方长春学校官网。

相关推荐

优能中学一对一

优能中学课程

长春初高中学习交流群

　　以上就是本文的全部内容，更多精彩内容，请持续关注长春新东方网。